Kako bi izgledao problem putujućeg trgovca da ga pustimo po gradovima po Srbiji? A kako bi izgledao da ga pustimo po svim poštama po Srbiji?
Umesto uvoda, želeo bih da se pohvalim – uspešno smo uneli sve pošte u Srbiji na OpenStreetMap platformu! Dobili smo odobrenje od “JP Pošte Srbije” da se pošte mogu koristiti kao otvoreni podaci, dogovorili smo se oko tagova, pokrenuta je akcija i izgruvali smo sve za 2-3 meseca! Sve je vodio Vanja Komadinović, pomogla je i hrvatska OSM zajednica ustupanjem Tasking Manager-a, a popeli smo se sa 460 unesenih pošti (sa diskutabilnim lokacijama i imenima) na 1460 i kusur pošta po Srbiji. Ovo je samo po sebi ogroman uspeh vredan blog posta za sebe, ali htedoh od tih podataka nešto i da napravim. I pomislio sam – za koliko li mogu da se obiđu sve pošte u Srbiji i kako ih je najbolje obići:) Naravno, ovo je čuveni “traveling salesman” problem, pa hajde sa tim znanjem da vidimo kako poštar da proputuje Srbiju:)
Obilazak gradova po Srbiji
Pre nego što naučiš da trčiš, prvo moraš da naučiš da hodaš, što kažu braća Englezi. Umesto da napadnemo problem 1460 pošta, hajde da krenemo laganije. Uzmimo 17 najvećih gradova po Srbiji (recimo preko 50.000 stanovnika u užem centru grada, ali metrika je poluslučajna, izvinite ako nema baš vašeg grada) – pitanje je koliko treba da ih obiđemo. Pre nego što rešimo ovaj problem, prvo da vidimo šta nam treba – treba nam da napravimo graf gde su čvorovi gradovi, graf treba da je kompletan i usmeren, a težine grana u grafu su vremena putovanja. Dakle, treba nam neki routing engine koji može da nam izračuna sve puteve između svih gradova brzo i jeftino (jeftino jer pričamo da ćemo morati posle da računamo 1460 x 1460, tj. preko 2 miliona ruta) i treba nam nešto što će na osnovu ovog grafa da izračuna najkraći put kroz isti.
Za routing engine sam uzeo Graphhopper – ne znam da li je najbolji, ali je takav da svako može da ga podesi lokalno relativno lako. Pokrenut sa celom Srbijom ne zauzima mnogo RAM-a (5-6GB), a rezultate uglavnom vraća u milisekundama. Pošto već radim u Python-u, za graf biblioteku sam iskoristio NetworkX. Pre nego nađemo najkraću putanju za sve gradove, hajde prvo da definišemo sve lokacije:
locations = [ (44.817852, 20.456833, 'Beograd'), (45.255034, 19.844935, 'Novi Sad'), (43.321228, 21.895924, 'Nis'), (44.012621, 20.918854, 'Kragujevac'), (42.995153, 21.946199, 'Leskovac'), (46.100078, 19.665399, 'Subotica'), (45.380306, 20.390582, 'Zrenjanin'), (44.870865,20.640092, 'Pancevo'), (43.891282,20.349748, 'Cacak'), (43.141062,20.517697, 'Novi Pazar'), (43.723559,20.687277, 'Kraljevo'), (44.664937,20.927356, 'Smederevo'), (44.270864, 19.886262, 'Valjevo'), (43.582629,21.326566, 'Krusevac'), (42.555673,21.897608, 'Vranje'), (44.756941,19.695826, 'Sabac'), (43.856440,19.840289, 'Uzice') ] |
OK, sad hajde da definišemo graf i da ga popunimo sa svim vremenima između ovih gradova:
def main(): http = urllib3.PoolManager() G = nx.DiGraph() for i, start_loc in enumerate(locations): for j, end_loc in enumerate(locations): if i == j: # We are not interested in time to get to ourselves continue resp = http.request('GET', f'http://localhost:8989/route?point={locations[i][0]},{locations[i][1]}&point={locations[j][0]},{locations[j][1]}&points_encoded=false&profile=car') json_obj = json.loads(resp.data.decode('utf-8')) travel_time_seconds = json_obj['paths'][0]['time'] / 1000 gpx = json_obj['paths'][0]['points']['coordinates'] G.add_edge(i, j, weight=travel_time_seconds, gpx=gpx) |
Pravimo “DiGraph” (directed graph), preskačemo da računamo veze iz istog grada u isti grad (petlje grafa) i kad god izračunamo rutu, sačuvamo i vreme (u “weight” svojstvu) i spisak koordinata kroz koje prolazimo (u “gpx” svojstvu, da ga ne računamo kasnije opet). Sad na ovom grafu nađemo najbrži obilazak kroz graf i potrebno vreme:
shortest_route = traveling_salesman.traveling_salesman_problem( G, cycle=True) total_travel_time_seconds = 0 for i, j in zip(shortest_route, shortest_route[1:]): total_travel_time_seconds += G[i][j]['weight'] print(f'Time: {total_travel_time_seconds/(60*60)}h, path: {[locations[i][2] for i in shortest_route]}') |
Kad imamo listu svih čvorova koje treba obići, možemo i da izgenerišemo GPX fajl koji možemo kasnije da vizuelizujemo:
import geojson geom_coll = [] for i, j in zip(shortest_route, shortest_route[1:]): geom_coll.append(geojson.Feature( geometry=geojson.LineString(G[i][j]['gpx']), properties={})) route = geojson.FeatureCollection(geom_coll) with open('route-cities.geojson', 'w') as output_json: geojson.dump(route, output_json) |
Eto, u manje od 50 linija koda – rešen problem:) Šta ti je kad su ti sve biblioteke na gotovs! Ne znam ko se seća, ali kad sam ja bio mali (kasne 80-te, rane 90-te) bile su mape koje su na poleđini imale rupe kao matrica, i kako pomeraš papir unutra, možeš da vidiš udaljenosti svakog grada od svakog drugog u SFRJ. E, pa ovo je to slično:)
Da ne davim više, evo odgovora na pitanje koje smo svi čekali – da bi se obišli centri svih gradova potrebno je:
- putovati ukupno 1799km
- ili vremenski 24h 16 min
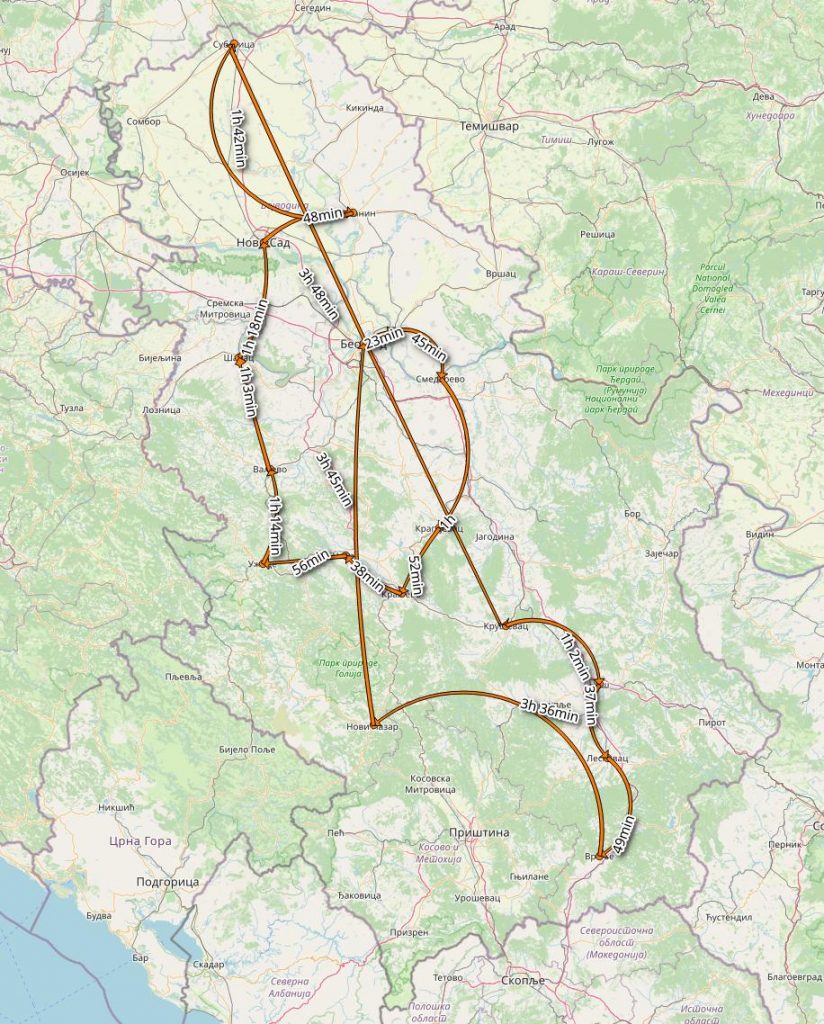
- ili redosledom: Beograd, Pančevo, Smederevo, Kragujevac, Kraljevo, Čačak, Užice, Valjevo, Šabac, Novi Sad, Zrenjanin, Subotica, Kruševac, Niš, Leskovac, Vranje, Novi Pazar, i nazad Beograd
Interesantno je da se na “Miloš Veliki” ulazi samo jednom i to u povratku, dok se E75 dosta više koristi (dosta više u odnosu na njihove dužine), a evo i najboljeg renderinga koji sam mogao da izvučem za 5 minuta (klik za veću verziju):
Mada… rekao bih da video dosta lepše to prikazuje, pa pogledajte njega bolje:
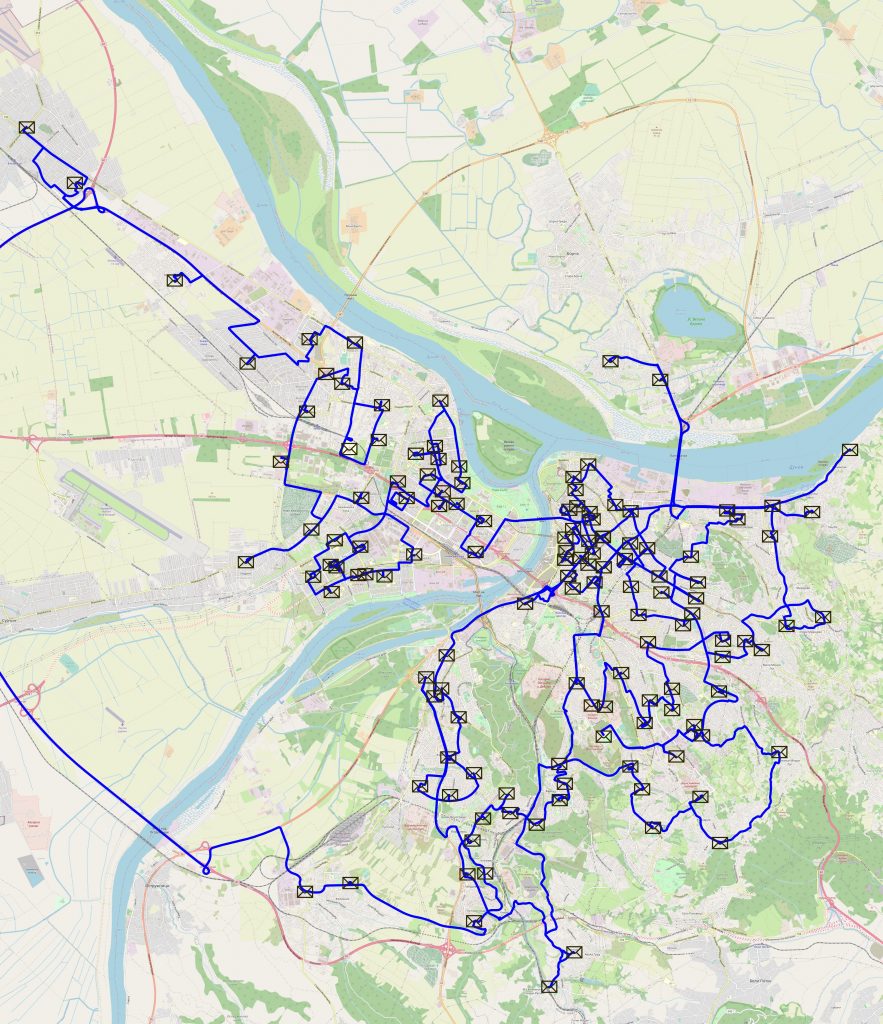
Pošte po Beogradu
OK, sad kad smo rešili taj problem, kako bi izgledalo da se obiđu sve pošte po Beogradu (užem centru). Njih ima “samo” 135. Uz malo duže računice, dolazimo do 6h 38 min ili 305 km, a evo kako bi ta putanja izgledala, ako vam je ovde išta jasno:)
Putujući poštar po Srbiji
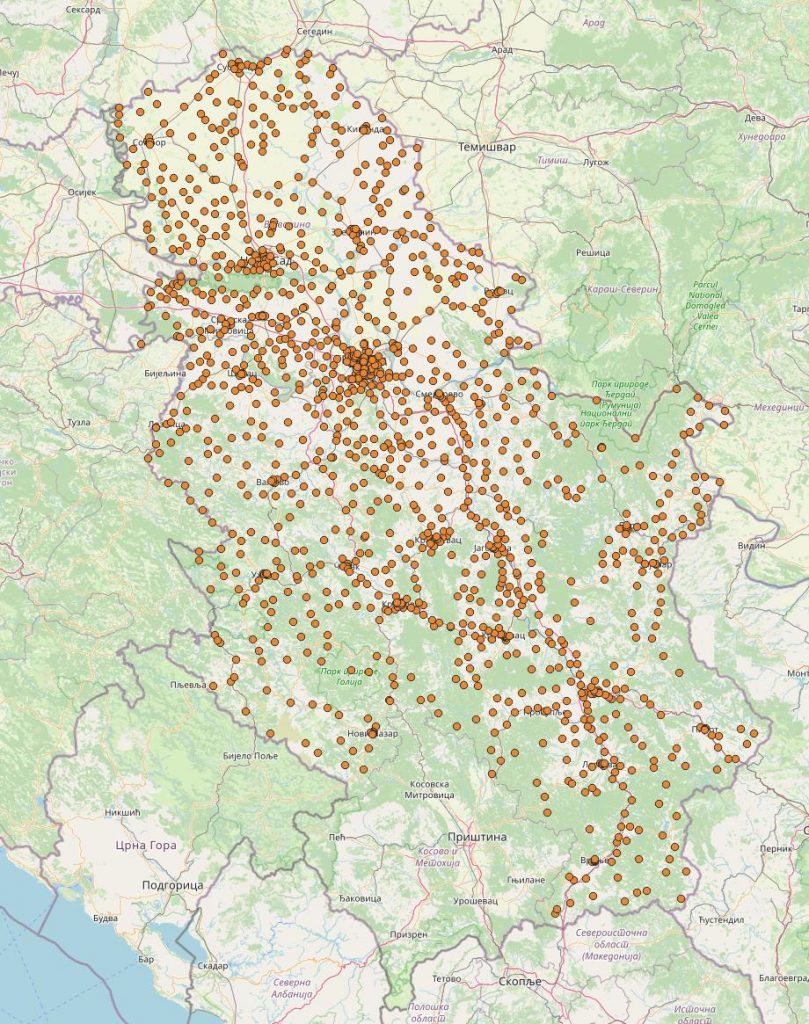
Eh, sad, hajmo sve ovo isto, ali za sve pošte u Srbiji, tj. za svih 1460. Da bismo izračunali 1460 x 1460 ruta, potrebno je oko 1.5 dana generisanja ruta na mojoj osrednjoj mašini. Posle toga treba još pola sata za rešavanje problema putujućeg poštara, ali kada želiš da menjaš parametre zato što si n00b i nemaš pojma šta radiš i mrzi te da čitaš NetworkX dokumentaciju, onda ti treba mnogo više jer probaš sve vrednosti svakog parametra, pa se tih pola sata lako pretvori u 3 dana:) Onda izgubiš još 3 dana da u QGIS-u izrenderuješ sve frejmove da napraviš video:) Da shvatite ceo posao oko uvoza pošti koji smo imali i da vidite stvarno za šta treba uraditi problem putujećeg poštara, evo svih pošti u Srbiji:
Mnogo pošti, zar ne?:)
Na kraju je algoritam izračunao da za obilazak treba celih 285 sati bez spavanja, odlazaka na pumpu i sličnih trivijalnosti i ukupno pređenih 14900 kilometara! Iskreno, imam neki osećaj u stomaku da ovo ipak nije najkraći put pošto stalno ide gore-dole (sever-jug), ali pošto ne mogu da rešavam NP probleme, moraću da se zadovoljim da je ovo empirijski najbolje što znamo danas (dok neko ne dokaže suprotno:). Ceo put izgleda nekako ovako – pustite ovo, naslonite se i uživajte:
Dodatak: očigledno algoritam koji sam koristio ovde nije baš toliko loš. Našao sam u divljini ovaj random poster – problem je rasprostranjeniji nego što sam mislio:)

[…] и нисмо знали шта да очекујемо (да будемо искрени, имали смо пре тога акцију уношења пошти, али размера проблема није ни […]